K Value Table Statistics

The real statistics resource pack contains the following function.

K value table statistics. The nth k statistic k n is the unique symmetric unbiased estimator of the cumulant kappa n of a given statistical distribution i e k n is defined so that k n kappa n 1 where x denotes the expectation value of x kenney and keeping 1951 p. Standard normal distribution table comes handy. The article mentions that k values are a convenient way of. If you noticed there are two z tables with negative and positive values.

The value of k 1 can also be computed using the inverse cumulative distribution function for the non central t distribution. They depend on the form of the distribution the size of your sample the confidence you want in your answer and the fraction of the population you want to fall within your interval. K value of the polystyrene boards and their thickness 1 2 inch k value and thickness of the wood siding materials c value of the outdoor air film the lower the u value the lower the rate of heat flow for a given set of conditions. They then took that value to a k value table to determine the sample size.

K factors can be tricky to compute. In the kolmogorov smirnov table the critical value of d increases as alpha 1 p decreases for a given n. A well insulated building wall. K value or k value may refer to.

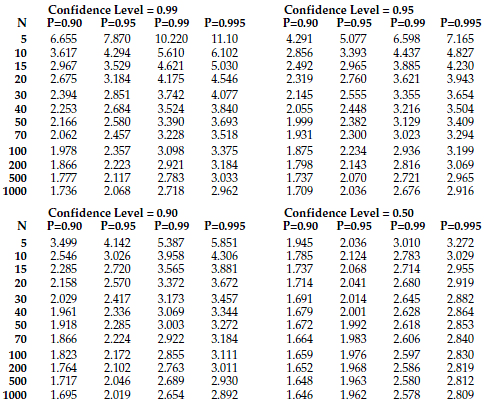
Tolerance norm n p α type k value of the tolerance interval for a normal distribution actually k for the two sided interval n sample size p α. This would imply that if a sample k s statistic is the critical d value at say the 05 level then it must also be the critical d value at the 01 level. What i don t understand is where did the k value table come from. This method may give more accurate results for small values of n.

That s where z table i e. I can t find it in any of my statistics books or on the web. For example suppose a machi.